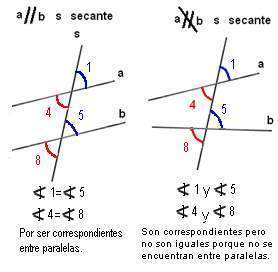
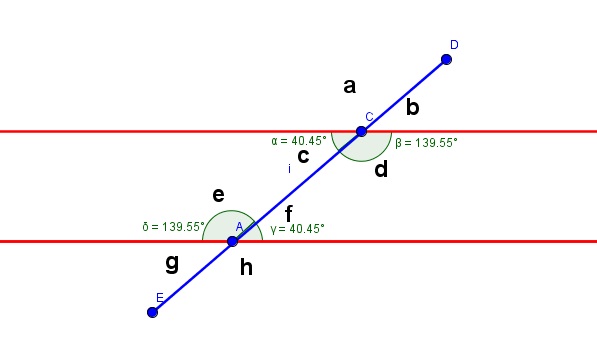
Los ángulos entre rectas paralelas y una transversal , en geometría euclidiana, son los ocho ángulos formados por dos rectas paralelas (r y s en la imagen de la derecha) y una transversal a ellas (t).
Denominación
- Ángulos alternos: son los que se encuentran a distinto lado de la secante.
- Ángulos conjugados: son los que se encuentran al mismo lado de la secante.
- Alternos internos: son los que se encuentran en la zona interior de las rectas paralelas.
- Alternos externos: Son los que se encuentran en la zona externa de las rectas paralelas.
- Correspondientes: Son los que se encuentran a un mismo lado de la secante, uno es externo y el otro interno.
Ángulos alternos internos
Las parejas de ángulos: c,f; d,e se llaman ángulos alternos internos.
Los ángulos alternos internos son congruentes.
Ángulos alternos externos
Las parejas de ángulos: a,h; se llaman ángulos alternos externos.
Los ángulos alternos externos son congruentes.
Ángulos conjugados internos
Los ángulos conjugados internos[1]son los que se encuentran del mismo lado de la secante y entre de las rectas paralelas.
Son ángulos conjugados internos los siguientes ángulos: c,e; d,f.
Los ángulos conjugados internos son suplementarios (suman ).
Ángulos conjugados externos
Los ángulos conjugados externos[1] son los que se encuentran al mismo lado de la secante y en la parte exterior de las rectas paralelas.
Son ángulos conjugados externos los siguientes ángulos: a,g; b,h.
Los ángulos conjugados son suplementarios (suman ).
Ángulos correspondientes
Son los ángulos que se encuentran a un mismo lado de la secante, uno es externo y el otro interno, son adyacentes. Los pares de ángulos: c, g; a, e; d, h y b, f; son correspondientes
Los ángulos correspondientes son congruentes.
Ángulos congruentes entre paralelas
Los ángulos opuestos por el vértice son congruentes, de modo que, de los ocho ángulos formados entre dos paralelas y una transversal, hay únicamente dos distintos, que no son adyacentes.
Teoremas y resultados relacionados
La noción de ángulos correspondientes es la base de numerosos ejemplos y teoremas fundamentales de la geometría,[2] presente en los cursos de enseñanza media de las matemáticas.[Ver: Bibliografía] Es un resultado geométrico intuitivo conocido y manejado desde la antigüedad, de manera tanto práctica como teórica,[3] si bien es la ciencia griega, y en particular Euclides, en los Elementos (siglo III a. C.), quienes formalizan los conceptos y las nociones de un modo que ha permanecido casi sin variaciones hasta nuestros días.
Proposiciones de Euclides
La controversia sobre el V postulado alcanza la definición de los ángulos entre rectas paralelas y una secante desde el momento mismo de la elección de la noción de «rectas paralelas»: las que guardan siempre la misma distancia; las que no se encuentran; o bien las que forman ángulos congruentes al ser cortadas por una transversal.[4]
De Los Elementos de Euclides:
Independencia del V postulado
Los siguientes dos resultados (lógicamente equivalentes[5]) son independientes del V postulado de Euclides. La Proposición 16, por ejemplo, no se cumple en geometría elíptica.
De Los Elementos de Euclides:
Geometría no-euclidiana
En la geometría absoluta o la geometría esférica por ejemplo, el quinto postulado de Euclides no aplica, por lo que los ángulos entre rectas paralelas y una secante tienen propiedades diferentes.
Véase también
- Postulados de Euclides
- Quinto postulado de Euclides
- Paralelismo
- Perpendicularidad
- Geometría no euclídea
- Ángulo
- Lados y ángulos correspondientes
- Relaciones aritméticas entre ángulos:
- Ángulos congruentes
- Ángulos complementarios
- Ángulos suplementarios
- Ángulos conjugados
- Relaciones posicionales entre ángulos:
- Ángulos adyacentes
- Ángulos consecutivos
- Ángulos opuestos por el vértice
- Ángulos interiores y exteriores de un polígono
Notas y referencias
Bibliografía
- Quintero, Ana Helvia (1994). Geometría. UPR. ISBN 0-8477-2345-3. (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última).
- Guerrero G, Ana Berenice (2006). Geometría: desarrollo axiomático. ECOE. (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última).
- Tsijli, Teodora (2006). Geometría Euclídea II. EUNED. ISBN 9977-64-830-1. (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última).
- Polania Sagra, Claudia Marcela; Sánchez Zuleta, Carmen Cecilia (2 de 2007). «3.2». Un acercamiento al pensamiento geométrico (1 edición). Lorenza Correa Restrepo. p. 141. ISBN 9789589812907.
- Ibáñez Carrasco, Patricia; García Torres, Gerardo (6 de 2006). «1.4». Matemáticas II, Geometría Y Trigonometría (1 edición). Cengage Learning.
- Landaverde, Felipe de Jesús (1977). Curso de Geometría. Editorial Progreso. p. 46. ISBN 9684361157.
Enlaces externos
- Pierce, Rod. «Líneas paralelas y pares de ángulos».
- Transversal and its properties, sitio interactivo, (en inglés).
- Elementos de Euclides.